Теория очередей

Дать определение характеристикам прибытия линейных систем ожидания

Основные знания о линиях обслуживания называются теорией очередей.

Сервисные затраты возрастают при попытке фирмы увеличивать уровень сервиса. Менеджеры в таком сервисном центре могут варьировать мощность установкой машин и персонала на специальных сервисных станциях, предотвращать или сокращать излишне длинные очереди. На складах бакалейных магазинов менеджеры и служащие могут работать, когда это необходимо, за чековыми аппаратами. В банках и аэропортах частично занятые работники могут быть позваны на помощь. По мере совершенствования сервиса (например, его ускорение) уменьшаются затраты времени, расходуемые на ожидание обслуживания, что показано убывающей линией. Затраты ожидания могут отражать потерянную производительность рабочих, пока их инструменты или машины ожидают ремонта, или просто могут быть оценены затратами потери покупателей по причине плохого сер виса и длинных очередей. 3 таких сервисных системах (например, в неотложной «скорой помощи») цена долгого ожидания может быть невыносимо высока.

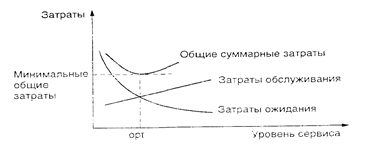
Рис. 1. Соотношение между затратами ожидания и сервисными затратами

Обзор трех частей линейных систем ожидания, или очередей:

1) прибытия, или входы системы;

2) дисциплина очереди, или собственно система ожидания;

3) сервисное оборудование.

Эти три компонента имеют определенные характеристики, которые должны быть изучены прежде, чем математические модели очереди могут быть разработаны.

Характеристики прибытия. Входной источник, который генерирует прибытия или клиентов сервисной системы, имеет три главные характеристики. Такими тремя важными характеристика ми являются размер источника, модели прибытия в систему очередей и поведения прибытия.

1. Размер источника. Размер прибытия рассматривается либо как неограниченный (практически бесконечный), либо как ограниченный (конечный). Когда число клиентов или прибытии в любой момент происходит лишь малыми порциями от числа потенциальных прибытии, источник прибытии рассматривается неограниченным, или бесконечным. В практической жизни приме рами неограниченных источников могут быть автомобили на автозаправках, покупатели в супермаркете, студенты, записывающиеся на занятия в большом университете. Большинство моделей очередей допускают такие неограниченные источники прибытии.

Пример ограниченного, или конечного, источника — это центр копирования только с восьмью копировальными аппаратами, которые могут выйти из строя и потребовать обслуживания.

2. Образец прибытии в систему. Заказчики приходят в пункт обслуживания либо по какому-то известному расписанию (напри мер, один пациент каждые 15 минут или один студент на консультацию каждые полчаса), либо случайным образом. Прибытия считаются случайными, если они независимы друг от друга и их появление невозможно точно предсказать.

Часто в теории очередей число прибытии за единицу времени может быть определено с помощью распределения вероятности, известного как распределение Пуассона. Для любого заданного количества –прибытий ( два заказчика в час или четыре грузовика в минуту) дискретное распределение Пуассона может быть определено формулой:

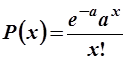для х=0, 1, 2, 3, 4 .

где Р (х) — вероятность х прибытии;

х — число прибытии в единицу времени;

а — среднее количество прибытии;

е— основание натурального логарифма 2,7183.

Поведение прибытии. Большинство моделей очередей полагают, что приходящие заказчики являются «терпеливыми». Терпеливые клиенты — это люди или машины, которые ожидают своей очереди до тех пор, пока их не обслужат, и не меняют очередь. К сожалению, жизнь сложнее, поскольку люди не всегда бывают терпеливыми. Клиенты, которые являются нетерпеливыми, отказываются присоединиться к очереди, потому что она слишком длинная, что не соответствует их запросам и интересам. Другая разновидность нетерпеливых клиентов — это те, которые, становясь в очередь, затем оказываются нетерпеливыми и покидают ее без завершения действия. Действительно, обе эти ситуации только подчеркивают необходимость теории очередей и анализа ожидания в очередях.

Дать определение характеристике очереди линейных систем ожидания